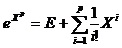Tutoriale pe aceasta tema:
- Librarie de functii si proceduri pentru lucru cu matrici (massive bidimensionale) in limbajul C si C++ – Intrare si iesire (post-ul contine si link catre arhiva cu codul sursa)
Acest tutoria include adunarea a doua matrice, inmultirea a doua matrice, transpunerea unei matrice, diferenta dintre doua matrice, inversa unei matrice ridicarea la putere a unei matrice etc.. Tot in aceasta clasa de proceduri sunt incluse si operatiile de adunare, scadere, inmultire si transpunere cu matrice vectorizate. De exemplu, suma a doua matrice vectorizate presupune transformarea matricelor in vectori, suma efectuandu-se acum intre doi vectori. Analog se realizeaza si scaderea, inmultirea si transpunerea matricei.
In continuare se prezinta procedurile care realizeaza operatiile specificate mai sus, precum si paralela intre modul de lucru cu o matrice alocata static si una alocata dinamic.
Operatia de inmultire a doua matrice este realizata in doua moduri:
- prin functia multiplying( n1, m1, x, n2, m2, y, z,*n3, *m3)din cadrul bibliotecii matrice.h;
- prin supraancarcarea operatorului “*” in cadrul clasei matrix.
Functia void multiplying(int n1,int m1,int x[30][30],int n2,int m2,int y[30][30],int z[30][30],int *n3,int *m3) realizeaza inmultirea a doua matrice rezultatul fiind obtinut intr-o a treia matrice. Parametrii functiei sunt urmatorii :
- int n1,m1– parametrii de intrare; reprezinta numarul de linii, respectiv numarul de coloane ale matricei x;
- int n2,m2– parametrii de intrare; reprezinta numarul de linii, respectiv numarul de coloane ale matricei y;
- int x[30][30],y[30][30]– parametrii de intrare; reprezinta matricele care vor fi inmultite;
- int z[30][30]-parametru de ieșire si reprezinta matricea rezultat al inmultirii celor doua matrice;
- int n3,m3– parametrii de iesire; reprezinta numarul de linii, respectiv numarul de coloane ale matricei rezultat z. Transferul acestor parametrii este realizat prin valoare.
Secventa care realizeaza inmultirea celor doua matrice este urmatoarea:
eror = 1;
if (m1 ! = n2)
eror = 0;
else
{
for (i = 0; i < n1; i++)
for (j = 0; j < m2; j++)
{
z[i][j] = 0;
for (k = 0; k < m1; k++)
z[i][j] += x[i][k] * y[k][j];
}
}
if (eror == 0)
printf("\n Multiplying is not possible!");
else
{
*n3 = n1;
*m3 = m2;
}
inmultirea a doua matrice se poate realiza decat daca numarul de coloane a primei matrice este egal cu numarul de linii a celei de-a doua. In functia prezentata mai sus, in cazul in care nu este indeplinita aceasta conditie, se afiseaza mesajul Multiplying is not possible!.
In clasa matrix operatia de inmultire este realizata prin supraancarcarea operatorului “*”. Functia de supraancarcare este urmatoarea:
matrix matrix::operator*(matrix b)
{
matrix c(n, b.m);
if (m == b.n)
{
for (i = 0; i < n; i++)
for (j = 0; j < b.m; j++)
{
c.a[i][j] = 0;
for (int k = 0; k < m; k++)
c.a[i][j] += a[i][k] * b.a[k][j];
}
}
return c;
}
Procedura de supraancarcare intoarce un obiect de tip matrix si anume rezultatul inmultirii celor doua matrice, care este creat in interiorul procedurii( obiectul c). Ea primeste ca parametru de intrare un obiect de tip matrix si anume obiectul b. El reprezinta operandul din partea dreapta a inmultirii. Operandul stang al inmultirii este dat de pionterul this. Ca si in cazul functiei din cadrul bibliotecii matrice.h si in cadrul procedurii de supraancarcare se verifica testul de validitate a inmultirii. Alocarea memorie pentru matricea rezultat c este realizata in momentul apelarii constructorului cu parametrii(matrix c(n,b.m)).
Suma a doua matrice este realizata in cadrul bibliotecii matrice.h si are denumirea adding(n1,m1,x,n2,m2,y,*n3,*m3,z). Functia are ca parametrii urmatoarele variabile:
- int n1,m1– parametrii de intrare; ei reprezinta dimensiunile matricei x(n1 numarul de linii, m1 numarul de coloane);
- int n2,m2– parametrii de intrare; ei reprezinta dimensiunile matricei y;
- int x[30][30],y[30][30]– parametrii de intrare; ei reprezinta matricele care sunt adunate;
- int *n3,*m3– parametrii de iesire; reprezinta dimensiunile matricei rezultat al adunarii matricei x cu matricea y(numarul de linii, respectiv numarul de coloane);
- int z[30][30]– parametru de iesire si reprezinta matricea rezultat al adunarii celor doua matrice.
Secventa de program care realizeaza suma celor doua matrice este urmatoarea:
eror = 1;
if ((n1 != n2) | (m1 != m2))
eror = 0;
else
{
for (i = 0; i < n1; i++)
for (j = 0; j < m1; j++)
z[i][j] = x[i][j] + y[i][j];
}
if (eror == 0)
printf("\n Adding is not possible!");
else
{
*n3 = n1;
*m3 = m2;
}
Ca si la inmultire la adunarea este necesara verificarea testului de validitate a sumei, adica numarul de linii si de coloane al celor doua matrice sa fie egal. In caz contrar se afiseaza urmatorul mesaj Adding is not posible!
Operatia de adunare este realizata in cadrul clasei matrix prin supraancarcarea operatorului “+”. Aceasta este realizata astfel:
matrix matrix::operator+(matrix b)
{
matrix c(n, m);
if ((n == b.n) && (m == b.m))
{
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
c.a[i][j] = a[i][j] + b.a[i][j];
}
return c;
}
Procedura primeste ca parametrii de intrare pionterul this si un obiect de tip matrix si anume b. Rezultatul adunarii este pus in obiectul c. Procedura este de tip matrix si intoarce astfel obiectul c. Ca si la inmultire pointerul this este operandul stang al adunarii, iar obiectul de tip matrix, b este operandul drept al operatiei.
Diferenta a doua matrice este realizata in cadrul bibliotecii matrice.h si are denumirea substracting(n1,m1,x,n2,m2,y,*n3,*m3,z). Ea are ca parametrii urmatoarele variabile:
- int n1,m1– parametrii de intrare; ei reprezinta dimensiunile matricei x(n1 numarul de linii, m1 numarul de coloane);
- int n2,m2– parametrii de intrare; ei reprezinta dimensiunile matricei y;
- int x[30][30],y[30][30]– parametrii de intrare; ei reprezinta matricele ale caror diferenta este efectuata ;
- int *n3,*m3– parametrii de iesire; reprezinta dimensiunile matricei rezultat al diferentei matricei x cu matricea y(numarul de linii, respectiv numarul de coloane);
- int z[30][30]– parametru de iesire si reprezinta matricea rezultat al scaderii celor doua matrice.
Secventa de program care realizeaza diferenta celor doua matrice este urmatoarea:
eror = 1;
if ((n1 != n2) | (m1 != m2))
eror = 0;
else
{
for (i = 0; i < n1; i++)
for (j = 0; j < m1; j++)
z[i][j] = x[i][j] - y[i][j];
}
if (eror == 0)
printf("\n Substraction is not possible!");
else
{
*n3 = n1;
*m3 = m2;
}
Analog inmultirii, la scadere este realizat testul de validitate a sumei, adica numarul de linii si de coloane al celor doua matrice sa fie egal. In caz contrar se afiseaza urmatorul mesaj Substraction is not possible!
Operatia de scadere este realizata in cadrul clasei matrix prin supraancarcarea operatorului “-”. Aceasta este realizata astfel:
matrix matrix::operator-(matrix b)
{
matrix c(n, m);
if ((n == b.n) && (m == b.m))
{
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
c.a[i][j] = a[i][j] - b.a[i][j];
}
return c;
}
Procedura primeste ca parametrii de intrare pointerul this si un obiect de tip matrix si anume b. Rezultatul scaderii este reprezentat de obiectul c. Procedura este de tip matrix si intoarce astfel obiectul c. Pointerul this este operandul stang al diferentei, iar obiectul de tip matrix, b este operandul drept al operatiei de scadere.
Operatia de transpunere a unei matrice este realizata in doua moduri:
- prin functia transpose( n, m, x, *n1, *m1, y)din cadrul bibliotecii matrice.h;
- prin supraancarcarea operatorului “!” in cadrul clasei matrix.
Functia void transpose(int n,int m,int x[30][30],int *n1,int *m1,int y[30][30]) realizeaza transpunerea unei matrice rezultatul fiind obtinut in alta matrice. Parametrii functiei sunt urmatorii :
- int n,m– parametrii de intrare; reprezinta numarul de linii, respectiv numarul de coloane ale matricei x;
- int x[30][30]– parametru de intrare si reprezinta matricea care este transpusa;
- int *n1,*m1– parametrii de iesire; reprezinta numarul de linii, respectiv numarul de coloane ale matricei x transpunse si anume a matricei y. Transferul este realizat prin valoare;
- int y[30][30]-parametru de iesire si reprezinta matricea rezultat al transpunerii matricei;
Secventa care realizeaza transpunerea matricei x este urmatoare:
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
y[j][i] = x[i][j];
*n1 = m;
*m1 = n;
In clasa matrix operatia de transpunere este realizata prin supraancarcarea operatorului “!”. Supraancarcarea este realizata astfel:
matrix matrix::operator!()
{
matrix b(n, m);
int i, j;
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
b.a[j][i] = a[i][j];
return b;
}
Procedura de supra-incarcare intoarce un obiect de tip matrix si anume rezultatul transpunerii matricei, care este creat in interiorul procedurii( obiectul b). Ea primeste ca parametru de intrare un pointer la un obiect de tip matrix si anume pointerul this. El reprezinta operandul din partea dreapta a transpunerii. Alocarea memorie pentru matricea rezultat c este realizata in momentul apelarii constructorului cu parametrii(matrix b(n,m)).
Ridicarea la putere a matricei este urmatoare operatie prezentata. Pentru obtinerea rezultatului dorit, pe langa functia propriu-zisa de ridicare la putere a unei matrice, sunt necesare functiile de copiere a unui masiv bidimensional intr-o matrice respectiv functia de inmultire a doua matrice. Aceasta din urma a fost prezentata in acest tutorial si de aceea reluarea ei nu este necesara.
Functia de copiere a unei matrice intr-o alta matrice din cadrul bibliotecii matrice.h este void copy(int n,int m, int x[30][30], int *n1,int *m1, int y[30][30]). Parametrii acestei functii sunt urmatorii:
- int n, int m – parametrii de intrare si reprezinta dimensiunile matricei X;
- int x[30][30] – parametru de intrare; reprezinta matricea ale carei elemente sunt copiate in masivul y;
- int *n1, int *m1 – parametrii de iesire si reprezinta dimensiunile masivului in care se copiaza matricea x. Transferul este realizat prin valoare.
- int y[30][30] – parametru de iesire si reprezinta matricea rezultat al copierii.
Functia este urmatoarea:
void copy(int n,int m, int x[30][30], int *n1,int *m1, int y[30][30])
{
int i,j;
for (i=0;i<n;i++)
for (j=0;j<m;j++) y[i][j]=x[i][j];
*n1=n;
*m1=m;
}
In clasa matrix copierea unei matrice intr-o alta matrice este realizata prin supraancarcarea operatorului “=”. Supraincarcarea se realizeaza astfel:
matrix &matrix ::operator=(matrix b)
{
for (i = 0; i < b.n; i++)
for (j = 0; j < b.m; j++)
a[i][j] = b.a[i][j];
n = b.n;
m = b.m;
return *this;
}
unctia intoarce un obiect de tip matrix, care este transferat prin referinta( in exemplul de mai sus acest obiect este pointerul this). Parametrul de intrare este reprezentat de obiectul b, iar paramerul de iesire este pointerul this.
Ridicarea la putere a unei matrice se realizeaza in functia void power(int n,int m,int x[30][30],int power,int *n2,int *m2, int y[30][30]) din cadrul bibliotecii matrice.h.
Functia primeste urmatorii parametrii:
- int n, int m – parametrii de intrare si reprezinta dimensiunile matricei x;
- int x[30][30] – parametru de intrare; reprezinta matricea care este ridicata la putere;
- int power – parametru de intrare si reprezinta puterea la cer va fi ridicata matricea;
- int *n1, int *m1 – parametrii de iesire si reprezinta dimensiunile masivului rezultat al ridicarii la putere a lui x. Transferul este realizat prin valoare;
- int y[30][30] – parametru de iesire si reprezinta matricea rezultat al ridicarii la putere.
Functia are urmatoarea structura:
copy(n, m, x, &n1, &m1, temp);
if ((power != 0) && (power != 1))
{
for (i = 1; i < power; i++)
{
multiplyng(n1, m1, temp, n, m, x, y, n2, m2);
copy(*n2, *m2, y, &n1, &m1, temp);
}
}
else if (power == 0)
{
*n2 = n;
*m2 = m;
creating_unit_1(*n2, *m2, y);
}
else
copy(n, m, x, n2, m2, y);
In cazul in care utilizatorul doreste ridicarea matricei la puterea zero, se obtine drept rezultat matricea unitate. Daca puterea este unu atunci matricea rezultat este chiar matricea x.
In clasa matrix operatia de ridicare la putere a unei matrice se realizeaza cu functia void matrix::power(int p, matrix b). Matricea de ridicat la putere este reprezentata de pointerul this catre un obiect de tip matrix. Deci acesta reprezinta un parametru de intrare, precum si puterea la care este ridicata matricea( int p) este parametru de intrare. Parametrul de iesire este reprezentat de obiectul de tip matrix, si anume b, care este matricea rezultat prin ridicarea la putere a matricei reprezentate de pointerul this.
Functia este urmatoarea:
void matrix::power(int p, matrix b)
{
matrix temp(n, m);
temp = *this;
if ((p != 0) && (p != 1))
{
for (i = 1; i < p; i++)
{
b = temp * (*this);
temp = b;
}
}
else if (p == 0)
b.creating_unit();
else
b = *this;
}
Functia, din cadrul bibliotecii matrice.h, void e(int n,int m,float x[30][30],int p,int *line,int *column,float e[30][30]) realizeaza ridicarea lui e( nu cel din lista de parametrii a functiei; este vorba despre e matematic) la puterea XP. Aceasta ridicare la putere se realizeaza dupa formula:
, unde E reprezinta matricea unitate.
Parametrii acestei functii sunt urmatorii:
- int n, int m – parametrii de intrare si reprezinta dimensiunile matricei X;
- float x[30][30] – parametru de intrare; reprezinta matricea din puterea lui e;
- int p – puterea la care se ridica matricea X;
- int *line, int *column – parametrii de iesire si reprezinta dimensiunile masivului rezultat al operatiei. Transferul este realizat prin valoare.
- float e[30][30] – parametru de iesire si reprezinta matricea rezultat a operatiei de ridicare la puterea XP a lui e .
Funcția are următoarea structura:
multiplyng_no_matrix_float(n, m, x, 1 / fact(1), &n1, &m1, y);
for (i = 2; i <= p; i++)
{
power_float(n, m, x, i, &n2, &m2, z);
multiplyng_no_matrix_float(n2, m2, z, 1 / fact(i), &n3, &m3, temp);
adding_float(n1, m1, y, n3, m3, temp, &n4, &m4, temp1);
copy_float(n4, m4, temp1, &n1, &m1, y);
}
creating_unit_1_float(n, m, unit);
adding_float(n, m, unit, n1, m1, y, line, column, e);
Dupa cum se observa se apeleaza functia multiplyng_no_matrix_float care realizeaza inmultirea unei matrice cu un numar. Datorita inmultirii matricei cu 1/(i!) este necesar ca matricea rezultat sa contina elemente de tip float. Functiile power_float, adding_float si copy_float sunt referite la sfarsitul acestui tutorial datorita particularitatii lor. Aceste functii au ca obiect de lucru matricele cu elemente de tip float. Functia creating_unit_1_float a fost prezentata in al doilea tutorial, http://www.itcsolutions.eu/2010/02/06/librarie-de-functii-si-proceduri-pentru-lucru-cu-matrici-masive-bidimensionale-in-limbajul-c-si-c-citire-si-afisare/ .
In clasa matrix functia membra care realizeaza aceasta operatie este:
void matrix::e(int p, matrix &er)
{
matrix b(n, m), c(n, m), temp(n, m), temp1(n, m), unit(n, m);
int l;
multiplyng_no_matrix(1 / fact(1), temp);
for (l = 2; l <= p; l++)
{
power(l, b);
b.multiplyng_no_matrix(1 / fact(l), c);
temp1 = temp + c;
temp = temp1;
}
unit.creating_unit();
er = unit + temp;
}
Aceasta functie primeste ca parametru de intrare pointerul this si puterea la care este ridicat obiectul de tip matrix reprezentat de pointerul this. Matrix &e este parametrul de iesire si reprezinta matricea obtinuta in urma ridicarii lui e la puterea AP, transferul realizandu-se prin referinta.
O mare aplicabilitate o are operatia de vectorizare a unei matrice. Aceasta este concretizata in lucrarea de fata, prin functia void matrix_line(int a[30][30],int n,int m,int x[],int *k) din cadrul bibliotecii matrice.h.
Aceasta functiei preia o matrice si o transforma intr-un vector de n*m+2 componente. Traversarea matricei se face pe linii, deci in vector regasirea elementelor matricei este echivalenta cu punerea cap la cap a fiecarei linii. Dimensiunea vectorului este cu doua componente mai mare decat numarul de elemente ale matricei deoarece pe ultimele doua pozitii se pastreaza numarul de linii, respectiv numarul de coloane ale matricei. Este importanta pastrarea dimensiunilor matricei pentru o eventuala operatie inversa( de la vector la matrice) sau pentru operatiile de adunare, scadere, transpunere si inmultire cu matrice vectorizate.
Functia primeste urmatorii parametrii:
- int a[30][30]– parametru de intrare si reprezinta matricea care este vectorizata;
- int n,m– parametrii de intrare; reprezinta dimensiunile matricei a;
- int x[]– parametru de iesire si reprezinta vectorul in care este transformata matricea a;
- int *k– parametru de iesire si reprezinta dimensiunea vectorului x. Transferul este realizat prin valoare.
Functia are urmatoarea structura:
void matrix_line(int a[30][30], int n, int m, int x[], int *k)
{
int i, j;
(*k) = 0;
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
{
x[*k] = a[i][j];
(*k)++;
}
x[*k] = n;
(*k)++;
x[*k] = m;
(*k) = (n * m) + 2;
}
In clasa matrix functia care realizeaza vectorizarea unei matrice se numeste matrix_line. Ea are urmatoarea forma int*
matrix_line(int &k). Functia este functie membra a clasei si are tipul int* returnand asadar un vector. Spre deosebire de functia matrix_line din biblioteca matrice.h in functia membra clasei atat vectorul cat si matricea sunt declarate dinamic. Asta presupune alocarea memorie in interiorul functiei pentru vectorul rezultant.
Functia este urmatoarea:
int *matrix::matrix_line(int *k)
{
int i, j, *x;
x = aloc_vec(n, m);
(*k) = 0;
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
{
x[*k] = a[i][j];
(*k)++;
}
x[*k] = n;
(*k)++;
x[*k] = m;
(*k) = (n * m) + 2;
return x;
}
Pentru a intelege mai bine algoritmul, se considera urmatorul masiv de 3 linii si 3 coloane:
1 2 3
4 5 6
7 8 9
Deci aceasta este matricea. In urma apelarii functiei matrix_line fie din biblioteca matrice.h, fie din clasa matrix se obtine urmatorul vector:
1 2 3 4 5 6 7 8 9 3 3
Dupa cum se observa apar doua componente diferite de elementele matricei. Ele reprezinta dimensiunile matricei si sunt intotdeauna memorate pe ultimele doua pozitii din vector, de unde si dimensiunea 3*3+2=11 componente.
Suma a doua matrice vectorizate este de asemenea realizata in doua moduri:
- matricele vectorizate sunt pointeri constanti, varianta din biblioteca matrice.h;
- matricele vectorizate sunt pointeri variabili, varianta din clasa matrix.
Prima varianta s-a concretizat prin functia void add_line_matr(int x[],int l1,int y[],int l2,int z[],int *k).
Functia primeste urmatorii parametrii:
- int x[],y[]– parametri de intrare si reprezinta matricele vectorizate care sunt insumate;
- int l1,l2– parametrii de intrare; reprezinta dimensiunile matricei vectorizate x, respectiv a matricei vectorizate y;
- int z[]– parametru de iesire si reprezinta vectorul in care sunt insumate cele doua matrice;
- int *k– parametru de iesire si reprezinta dimensiunea vectorului z. Transferul este realizat prin valoare.
Functia are urmatoarea structura:
void add_line_matr(int x[], int l1, int y[], int l2, int z[], int *k)
{
int i, j;
*k = 0;
if ((x[l1 - 2] == y[l2 - 2]) && (x[l1 - 1] == y[l2 - 1]))
{
for (i = 0; i < l1 - 2; i++)
z[i] = x[i] + y[i];
z[i] = x[l1 - 2];
i++;
z[i] = x[l1 - 1];
*k = l1;
}
}
In clasa matrix functia care realizeaza insumarea a doua matrice vectorizate se numeste row_matrix_elem_sum. Ea are urmatoarea forma int* row_matrix_elem_sum( matrix ,int *,int *,int *). Functia este functie membra a clasei si are tipul int* returnand asadar un vector. Spre deosebire de functia add_line_matr din biblioteca matrice.h in functia membra clasei atat vectorul cat si matricea sunt declarate dinamic. Asta presupune alocarea memorie in interiorul functiei pentru vectorul rezultant.
Functia primeste urmatorii parametrii:
- parametrii de intrare : this, matrix b, int *x, int *y; ei reprezinta matricele care au fost vectorizate, respectiv vectorii in care au fost transformate;
- parametrii de iesire : int *k care reprezinta dimensiunea vectorului rezultat al adunarii vectorilor x si y.
Aceasta este functia:
int *matrix::row_matrix_elem_sum(matrix b, int *x, int *y, int *k)
{
int *z;
z = aloc_vec(n, m);
*k = 0;
if ((n == b.n) && (m == b.m))
{
for (i = 0; i < n * m; i++)
z[i] = x[i] + y[i];
z[i] = n;
i++;
z[i] = m;
*k = (n * m + 2);
}
return z;
}
Avem urmatorul exemplu:
A= 2 12 B= 6 14
3 1 43 5
Dupa vectorizare se obtine:
X=2 12 3 1 2 2
Y= 56 4 43 5 2 2
Dupa apelarea functiei add_line_matr(x,6,y,6,z,&k) se obtine matricea vectorizata Z=58 16 46 6 2 2
Operatia de scadere este realizata prin functiile void substr_line_matr (int x[],int l1,int y[],int l2,int z[],int k) din matrice.h si int*matrix::row_matrix_elem_substr( matrix b,int *x,int *y,int *k) din clasa matrix. Explicatiile sunt identice ca la operatia de adunare. Functiile sunt prezentate in anexa de la sfarsitul lucrarii.
Inmultirea a doua matrice vectorizate alocate static se realizeaza prin procedura void multiply_line_matr(int x[],int l1,int y[],int l2,int z[],int *k). Functia primeste urmatorii parametrii:
- int x[],y[]– parametri de intrare si reprezinta matricele vectorizate care sunt inmultite;
- int l1,l2– parametrii de intrare; reprezinta dimensiunile matricei vectorizate x, respectiv a matricei vectorizate y;
- int z[]– parametru de iesire si reprezinta vectorul in care sunt inmultite cele doua matrice;
- int *k– parametru de iesire si reprezinta dimensiunea vectorului z. Transferul este realizat prin valoare.
Functia are urmatoarea structura:
void multiply_line_matr(int x[], int l1, int y[], int l2, int z[], int *k)
{
int q, r, i, j, lineA, columnA, lineB, columnB;
int *v, *w, l, vb, vb1, matrix[30][30];
lineA = x[l1 - 2];
columnA = x[l1 - 1];
lineB = y[l2 - 2];
columnB = y[l2 - 1];
if ((columnA == lineB))
{
line_matrix(y, l2, matrix, &q, &r);
matrix_line(matrix, q, r, v, &l);
vb = 0;
*k = 0;
while (vb * columnA != (columnA * lineA))
{
j = 0;
for (i = (vb * columnA); i < ((vb + 1) * columnA); i++)
{
w[j] = x[i];
j++;
}
vb1 = 0;
while ((vb1 * lineB) != (lineB * columnB))
{
j = 0;
z[*k] = 0;
for (i = (vb1 * lineB); i < ((vb1 + 1) * lineB); i++)
{
z[*k] += w[j] * v[i];
j++;
}
vb1++;
(*k)++;
}
vb++;
}
z[*k] = lineA;
(*k)++;
z[*k] = columnB;
*k = columnB * lineA + 2;
}
else
*k = 0;
}
Este necesara retransformarea in matrice a vectorului y. Aceasta se realizeaza cu functia:
void line_matrix(int x[], int l, int a[30][30], int *n, int *m)
{
int i, j, p;
(*n) = x[l - 2];
(*m) = x[l - 1];
p = 0;
for (i = 0; i < *n; i++)
for (j = 0; j < *m; j++)
{
a[i][j] = x[p];
p++;
}
}
Dupa aceasta transformare se vectoriza matricea matrix obtinuta anterior prin apelarea functiei line_matrix(y,l2,matrix,&q,&r). Aceasta vectorizare este de fapt o transpunere a matricei matrix. Operatia se realizeaza cu functia void matrix_line_top(int a[30][30],int n,int m,int x[],int *k). Sau realizat aceste operatii pentru a usura algoritmul de inmultire a celor doua matrice vectorizate.
Algoritmul este simplu, folosindu-se variabilele vb si vb1 pentru a sti cand se termina componentele matricei. Altfel exista riscul inmultirii si ultimelor doua pozitii ale vectorilor.
Tot cu ajutorul acestor variabile se disting liniile si coloanele matricelor transpuse in vectorii x, respectiv y. Acest lucru este necesar pentru a obtine rezultatul dorit si anume o matrice sub forma vectoriala. Variabilele lineA, columnA sunt folosite pentru pastra numarul de linii, respectiv numarul de coloane al matricei transformate in vectorul x. Analog variabilele lineB, respectiv columnB.
In clasa matrix inmultirea a fost realizata in functia int * row_matrix_elem_multpl(matrix b,int *x,int *y,int k). Pentru a evita folosirea a multor variabile sunt folosite ca parametrii de intrare si cele doua matrice( pointerul this si matrix b), precum si vectorii in care au fost transformate int * x, respectiv int *y. Algoritmul este acelasi cu cel al functiei multiply_line_matr, cu mentiunea ca in clasa matrix vectorii sunt declarati dinamic si de aceea este necesara alocarea spatiului necesar fiecaruia.
Functia membra clasei este urmatoarea:
int *matrix::row_matrix_elem_multpl(matrix b, int *x, int *y, int *k)
{
int vb, vb1, **matrix, *v, *w, *z;
z = aloc_vec(m, b.n);
if ((m == b.n))
{
matrix = b.row_to_matrix(y);
v = b.row_matrix2(matrix);
vb = 0;
*k = 0;
while (vb * m != (n * m))
{
j = 0;
w = (int *)malloc(m * sizeof(int));
for (i = (vb * m); i < ((vb + 1) * m); i++)
{
w[j] = x[i];
j++;
}
vb1 = 0;
while ((vb1 * b.n) != (b.n * b.m))
{
j = 0;
z[*k] = 0;
for (i = (vb1 * b.n); i < ((vb1 + 1) * b.n); i++)
{
z[*k] += w[j] * v[i];
j++;
}
vb1++;
(*k)++;
}
vb++;
}
z[*k] = n;
(*k)++;
z[*k] = b.m;
*k = b.m * n + 2;
}
else
*k = 0;
return z;
}
Transpusa unei matrice vectorizate este folosita in functia de inmultire pentru a usura munca. Functia este urmatoarea:
void transpose_line_matrix(int x[], int k, int *z, int *l1)
{
int *v, a[30][30], q, r, l, i;
line_matrix(x, k, a, &q, &r);
matrix_line(a, q, r, v, &l);
for (i = 0; i < l - 2; i++)
z[i] = v[i];
z[i] = r;
i++;
z[i] = q;
(*l1) = q * r + 2;
}
Functia membra a clasei matrix este de tip int* si returneaza astfel vectorul obtinut in urma transpunerii matricei vectorizate. Ea primeste ca parametrii de intrare matricea vectorizata si dimensiunea vectorului. Functia este urmatoarea:
int *matrix::row_matrix_elem_transpose(int *x, int *k)
{
int **matrix, *v, *z;
z = aloc_vec(m, n);
*k = 0;
matrix = row_to_matrix(x);
v = row_matrix2(matrix);
for (i = 0; i < n * m; i++)
z[i] = v[i];
z[i] = m;
i++;
z[i] = n;
(*k) = n * m + 2;
return z;
}
Cum declararea variabilelor este realizata dinamic apare necesitatea alocarii spatiului de memorie pentru vectorul rezultat. Alocarea memorie se obtine prin intermediul functiei membre cu acces privat aloc_vec(int, int). Aceasta functie este urmatoarea:
int *matrix::aloc_vec(int n, int m)
{
int *pvec;
pvec = (int *)malloc((n * m + 2) * sizeof(int));
return pvec;
}
Aloca spatiul de memorie pentru un vector de dimensiunea n*m+2.
Datorita necesitatilor ulterioare sunt incluse in biblioteca matrice.h si functiile multiplying_float(&n,&m,x), adding_float(n,m,x), power_float(n,m,x,p,n1,m1,y). Diferenta dintre aceste functii si functiile prezentate in acest tutorial consta in faptul ca tipul elementelor matricei nu este intreg. Matricea este declarata astfel:
float x[30][30].
Asadar comentariile pentru aceste functii sunt identice cu cele corespondente functiilor prezentate in acest tutorial, care au ca parametru de intrare un masiv bidimensionl cu elemente intregi.
Functii prezentate in acest tutorial fac parte din grupul procedurilor de calcul care sunt utilizate in tutorialele urmatoarea pentru exemplificarea aplicabilitatii calculului matriceal.
Tutoriale pe aceasta tema: